[컴퓨터 구조] 에러 검출 코드
▶ 에러 제어 방식
수신 측에서는 송신 측에서 보낸 정보를 기초로 에러를 검사하여 자체 정정하거나 송신 측에 재전송을 요청한다. 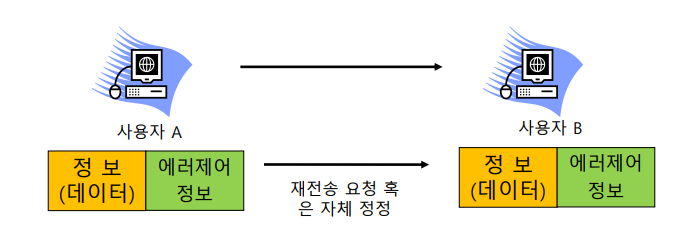
▷ FEC와 ARQ의 장단점
| FEC(전진 에러 수정) | ARQ(검출 후 재전송) | |
|---|---|---|
| 장점 | ① 수신 측에서 에러를 정정할 수 있다. ② 재전송을 하지 않아 대역폭 관리에 효율적이다. |
① 수신 측 정보에 에러정정부호를 삽입할 필요가 없으므로 구현이 간단하다. ② 프레임에 FCS만 붙는다. |
| 단점 | ① 에러정정부호의 삽입으로 프레임의 크기가 커진다. ② 구현이 어렵다. |
① 수신 측이 자체 에러정정을 못한다. ② 재전송에 드는 대역폭 손실이 크다. |
- 대역폭: 특정한 기능을 수행할 수 있는 주파수의 범위
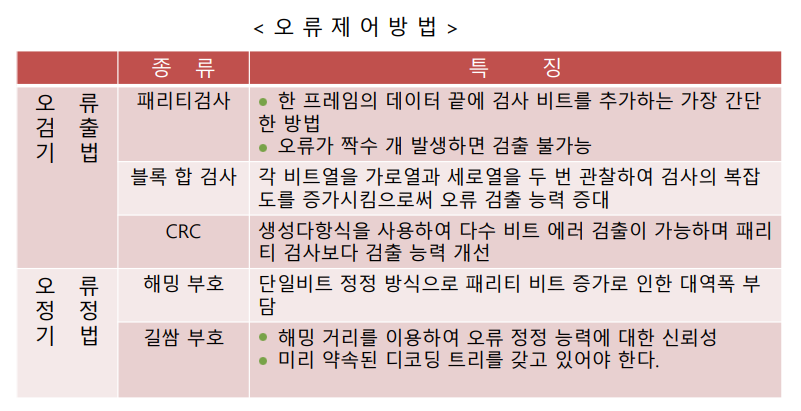
▼ 에러 검출 부호 사용 방식
송신 측에서 보내고자 하는 정보 이외에 별도의 잉여 데이터(에러 제어 코드)를 보내면 수신 측에서 잉여 데이터를 검사하는 방식으로 에러 검출을 한다.
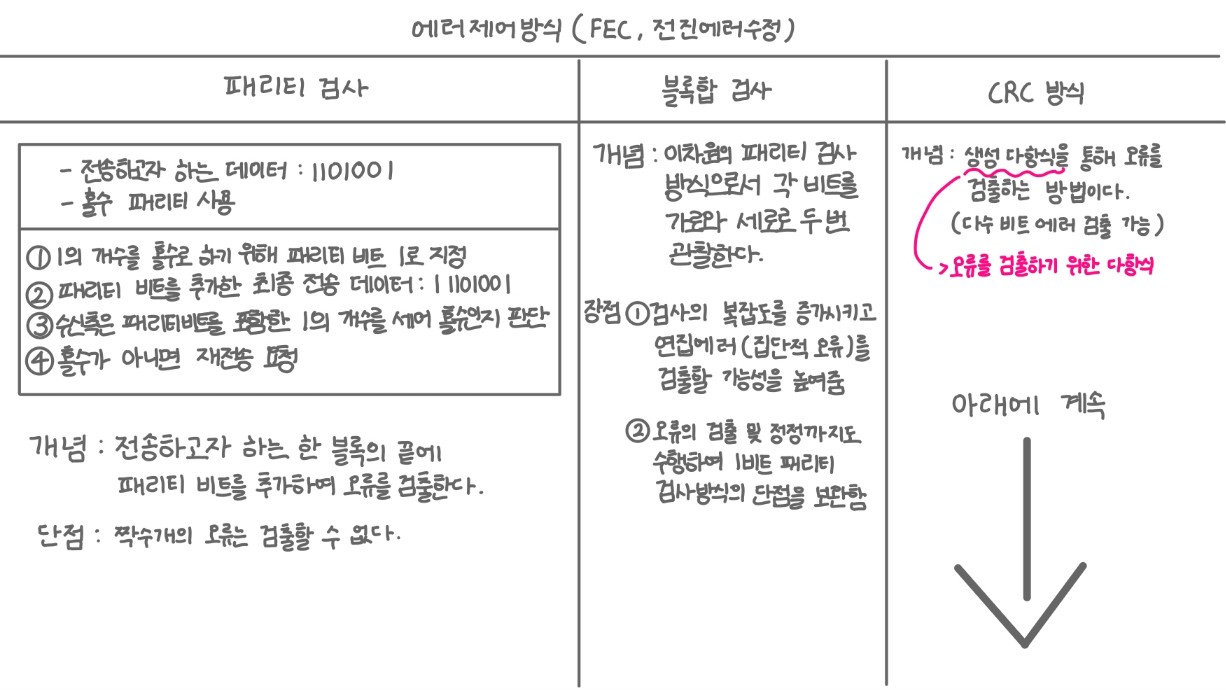
▷ 패리티 검사
개념
-
한 블록의 끝에 패리티 비트를 추가하여 오류를 검출한다.
-
홀수 패리티 방식과 짝수 패리티 방식으로 구분한다.
- 홀수 패리티는 1의 비트 수를 항상 홀수 개로 유지하는 반면 짝수 패리티는 1의 비트 수를 항상 짝수 개를 유지한다. 통신측과 수신측이 1의 비트 수가 홀수인지 짝수인지 알고 있어 오류 검출이 가능해진다.
홀수 패리티 사용 예시 ( 전송하고자 하는 데이터 : 1101001 )
① 1의 개수를 홀수로 하기 위해 패리티 비트를 1로 지정 ② 패리티 비트에 추가한 최종 전송 데이터 : 11101001 ③ 수신 측은 패리티 비트를 포함한 데이터 내에서 1의 개수를 세어 홀수인지 판단 ④ 홀수가 아니면 재전송을 요청
패리티 검사 단점
- 짝수 개의 오류는 검출 불가하다.
- ex ) 11011001 : 짝수 개의 오류가 발생하여, 1의 개수가 홀수인 경우
▷ 블록 합 검사
개념
-
1비트 패리티의 검사 방식의 단점을 보완 -> 오류의 검출 및 정정까지도 수행
-
이차원의 패리티 검사 방식으로서 각 비트를 가로와 세로로 두 번 관찰한다.
-
검사의 복잡도를 증가시키고 연집 에러(집단적 오류)를 검출할 가능성을 높여준다.
블록 합 검사 구현 예시(짝수 패리티 사용)
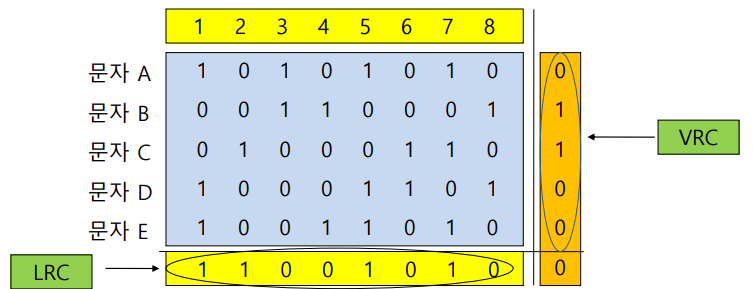
- VRC
- 수직 방향으로 패리티 비트를 부여하는 방식으로, 보통 패리티 검사라고 할 때 VRC를 가리킨다.
- 홀수 패리티, 짝수 패리티에 따라 1 또는 0으로 정하여 전송한다.
- 2개의 비트가 동시에 에러가 발생하면 검출이 불가능하다.
- LRC
- 수평 방향으로 패리티 비트를 부여하는 방식으로, 블록의 맨 마지막에 패리티 비트를 부여한다.
▷ CRC (순환 중복 검사)
개념
- 1비트의 에러 제어가 아니라 다수에 비트에 의해 에러를 제어하는 방식이다.
- 생성 다항식을 이용하여 에러를 검출한다.
- 생성 다항식: 오류를 검사하기 위한 다항식, 통신측과 수신측이 같이 알고 있는 정보
방식
① 보내려고 하는 메세지 값에 최고차수를 곱하고 그 값을 생성 다항식으로 나눈다. ② 결과로 나온 나머지 값으로 오류를 판정한다.
부호화 과정
- 각 비트들의 값을 보면서 하나의 함수를 만드는 과정
- 정보 비트를 전송 비트의 다항식에 의한 표현으로 변환
- 다항식을 2진수로 표현(계산)
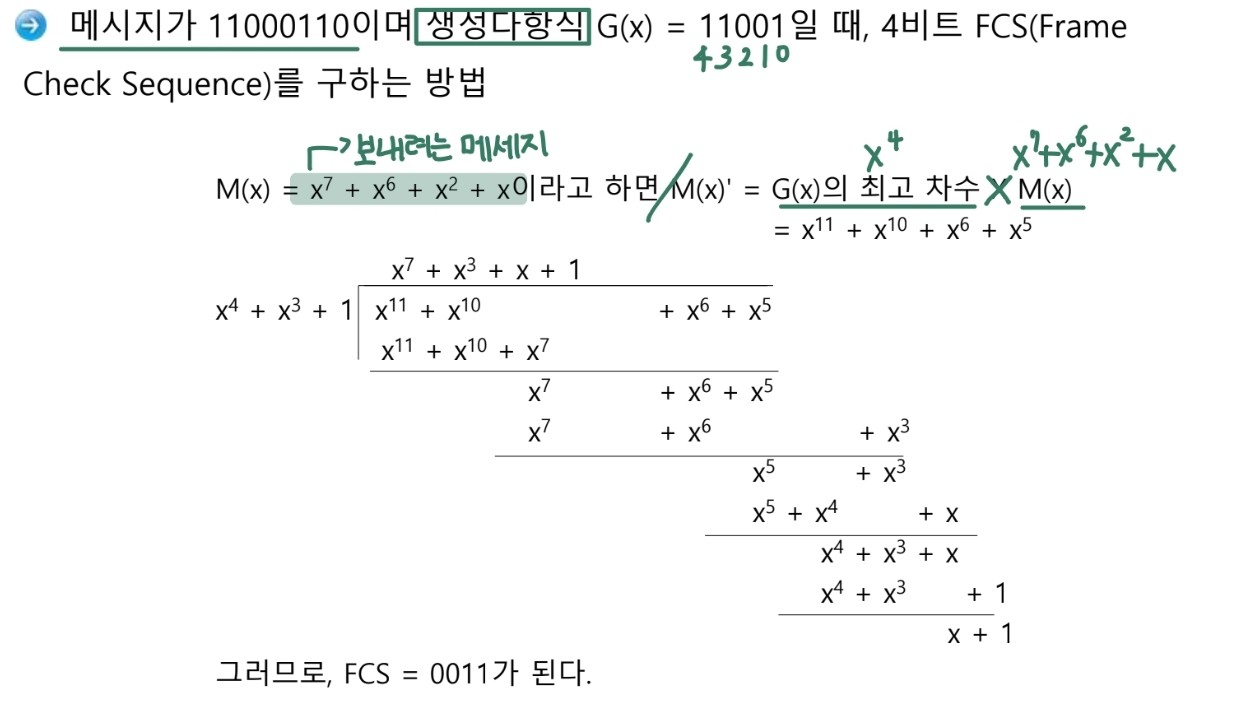
CRC 구현 예시 1
- 메시지가 11000110이며 생성다항식 G(x) = 11001일 때, 4비트 FCS(Frame Check Sequence)를 구하는 방법
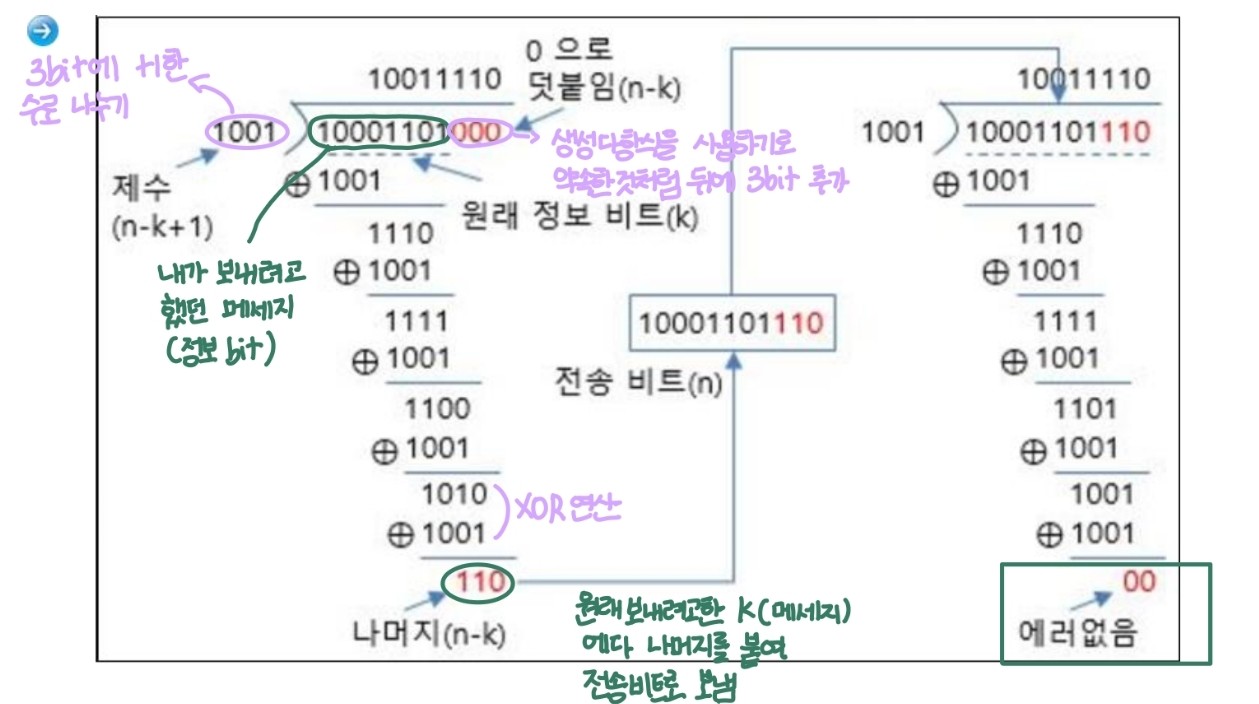
CRC 구현 예시 2
- 메세지가 10001110에 대한 신호를 CRC부호화를 위해 필요한 패리티 비트의 형태로 표현하시오.
(단, 생성 다항식 G(x) = x ⁵ + x³ + x² + x 이다.)

▼ 에러 정정 부호 사용 방식
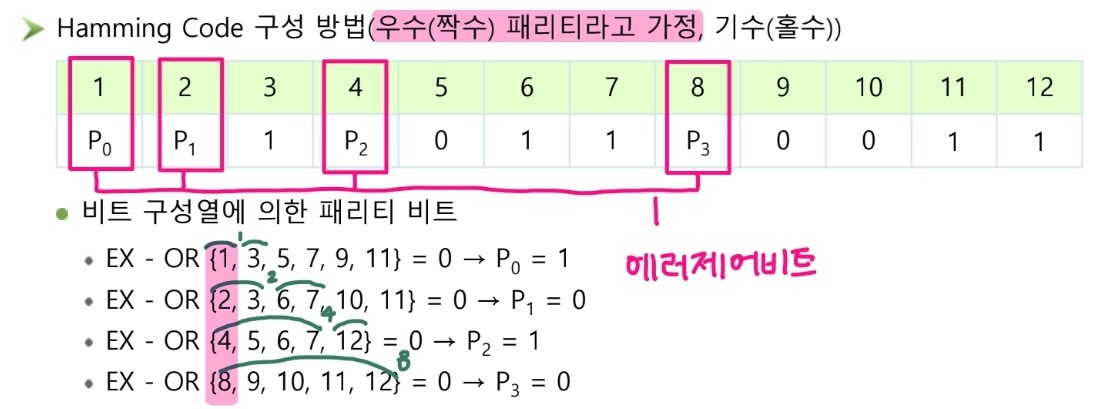
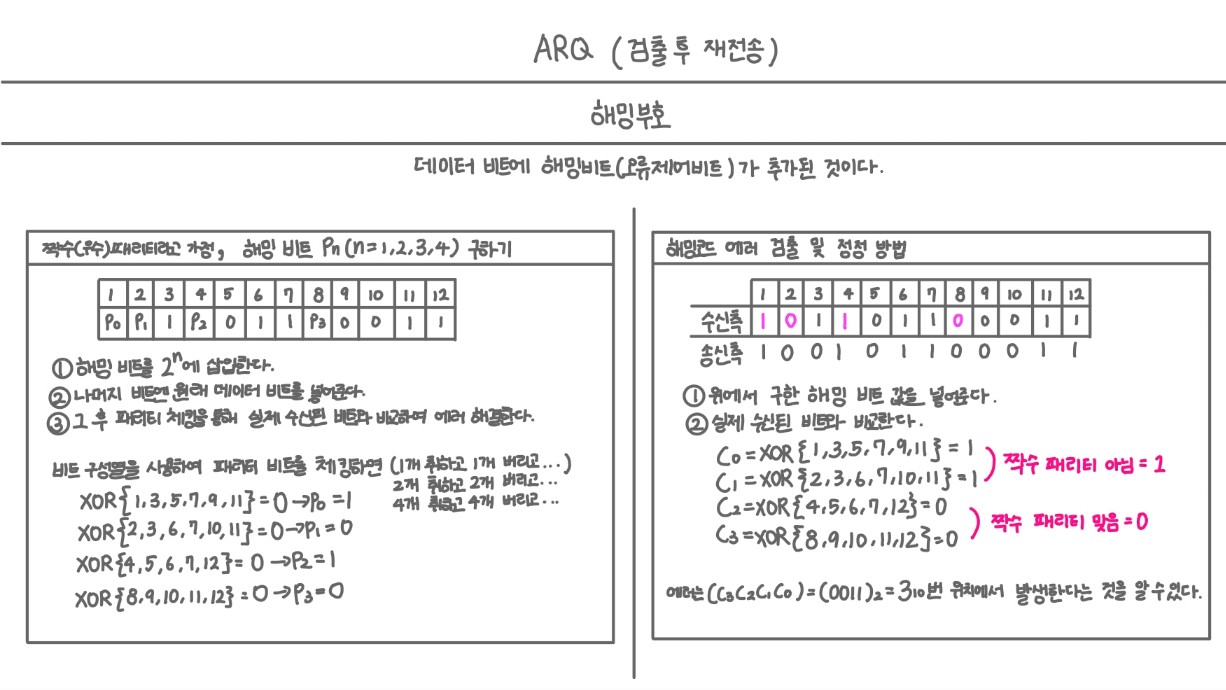
▷ 해밍 부호⭐
개념
- 에러를 검출하는데 필요한 잉여 데이터 비트수를 최소화 한 방법이다.
- n개의 정보비트와 k개의 해밍 비트로 운용된다.
- 즉, 데이터 비트에 해밍 비트(오류 체크 비트)가 추가된 것이다!
- 송신한 다음 오류가 발생해도 고쳐 쓸 수 있도록 해준다.
- 오류를 수정할 수 있도록 1,2,4,8…에 해당하는 비트에 수정할 수 있는 정보를 준다.
해밍비트는 어디에 삽입될까?
① 해밍 비트는 2n에 삽입된다. ② 나머지 비트엔 원래 데이터 비트를 넣어준다. ③ 그 후 패리티 체킹을 해준다.
패리티 체킹 방법 : 비트 구성열을 이용
- 1개 취하고 1개 버리고, 2개 취하고 2개 버리고, 4개 취하고… 이런 방식으로 패리티 비트를 체킹한다.
① 해밍 비트를 2n에 삽입한다.
② 나머지 비트엔 원래 데이터 비트를 넣어준다.
③ 그 후 패리티 체킹을 해준다.
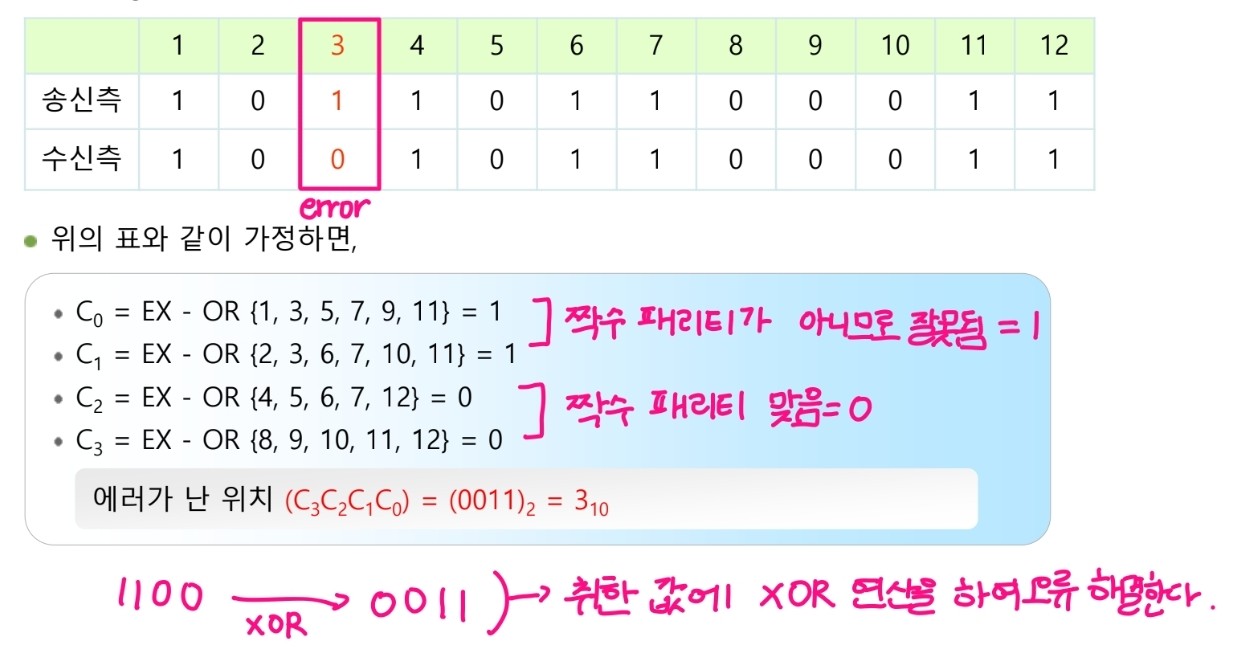
실제 수신된 체크 비트에 XOR 연산을 하여 오류를 해결한다.
🔖정리

📎참조
- 『 성결대학교 김자원 교수님 』 - 컴퓨터 구조 (2023)
- 『 컴퓨터구조(제5판) 』 - 복두 출판사
- https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=deepb1ue&logNo=221189953315

댓글남기기