[Algorithm/Java] 백준 1074번 - Z

---

https://www.acmicpc.net/problem/1074

---

📌 문제

문제 유형

• 분할 정복
• 재귀

문제 설명

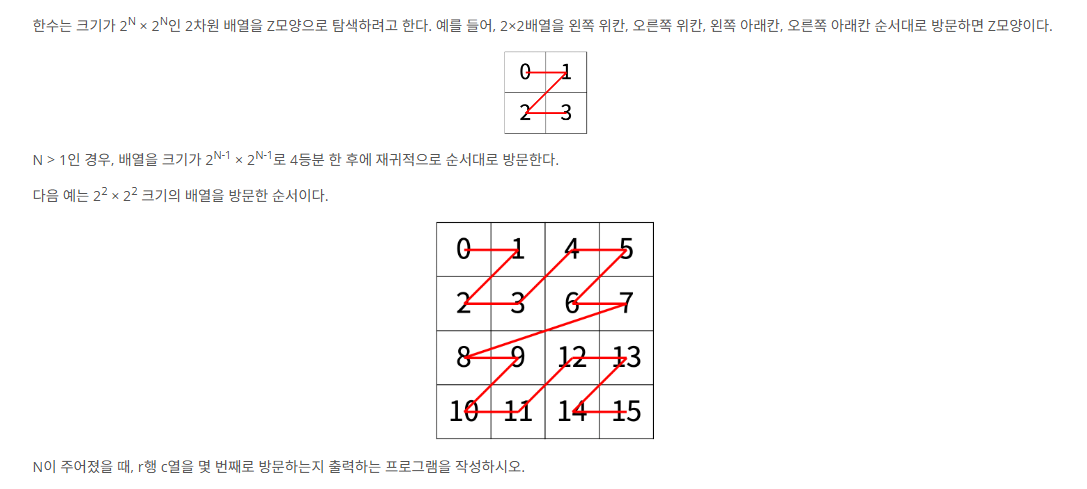
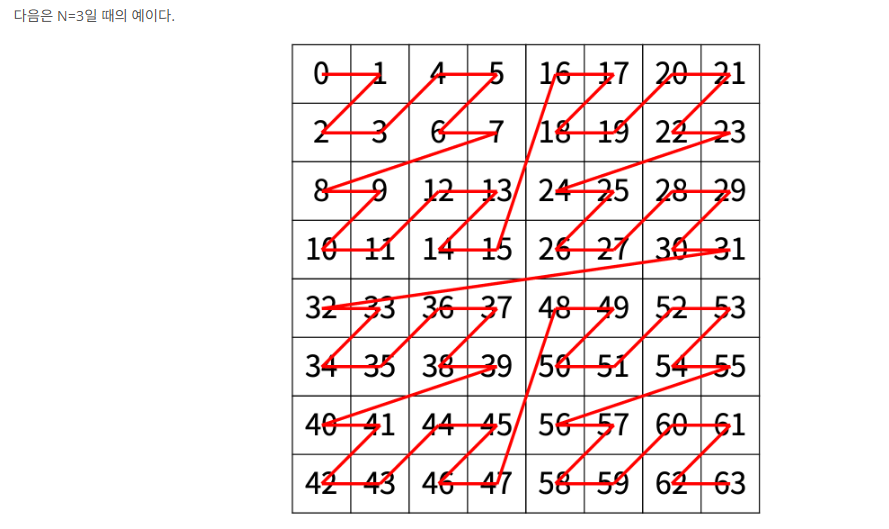
입력

첫째 줄에 정수 N, r, c가 주어진다.

2 3 1

출력

r행 c열을 몇 번째로 방문했는지 출력한다.

11

🔍 문제 풀이

• Z 순서는 반복적인 4분할 구조
• 한 번 분할할 때마다 1사분면 → 2 → 3 → 4 순서로 감
• (r, c)가 어느 사분면에 속해 있는지만 알면, 앞에 몇 칸 지나갔는지 계산할 수 있음
• 그 사분면 안에서 다시 계산 반복하면 됨

1. 2^N × 2^N 정사각형을 Z 순서로 방문하며, (r, c)가 몇 번째로 방문되는지 구한다.
2. Z(x, y, size) 함수는 현재 정사각형을 1~4사분면으로 분할한다.
3. 그 후, (r, c)가 속한 사분면을 찾아 그쪽으로만 재귀 호출한다.
4. 이때, 앞에 있는 사분면은 모두 건너뛰므로, cnt += half * half * 사분면번호로 계산해 누적한다.
5. size == 1이면 더 이상 쪼갤 수 없으므로, cnt을 출력한다.

사분면 구분 기준:

사분면	r 조건	c 조건
1사분면	r < x + half	c < y + half
2사분면	r < x + half	c ≥ y + half
3사분면	r ≥ x + half	c < y + half
4사분면	r ≥ x + half	c ≥ y + half

예시 (n = 2, r = 3, c = 1)

4×4 격자에서 (3,1)이 Z 순서로 몇 번째인지 찾기

1. 전체 4×4를 4조각으로 나누기
   • (3,1)은 3사분면 → 앞에 8칸 있음 → cnt += 8
2. 3사분면을 다시 4조각으로 나눔
   • (3,1)은 4사분면 → 앞에 3칸 있음 → cnt += 3

=> 더 쪼갤 수 없으므로 출력 → cnt = 11
=> 즉, (3,1)은 11번째로 방문됨

4x4 격자 기준 사분면 구간

사분면	행(r) 구간	열(c) 구간
1사분면	0 ~ 1	0 ~ 1
2사분면	0 ~ 1	2 ~ 3
3사분면	2 ~ 3	0 ~ 1
4사분면	2 ~ 3	2 ~ 3

건너뛸 때 cnt += half * half * N을 더하는 이유

• cnt를 통해 “지금까지 몇 칸 지나왔는지”를 저장 중
• 만약, 지금 (r, c)가 3사분면이면 앞에 1사분면 + 2사분면 총 2개를 지나왔음
• 각 사분면은 half * half 크기니까

cnt += half * half * 2;

// 예시: size = 4 (4x4 격자)
 0  1 | 4  5
 2  3 | 6  7
------|------
 8  9 |12 13
10 11 |14 15

지나온 총 칸 수만큼 cnt에 더해줘야 현재 사분면의 시작 번호가 맞다.

💻 전체 코드

재귀

변수	의미
size	현재 정사각형의 한 변의 길이
half	size / 2, 4등분을 위한 기준점
half*half	한 사분면의 칸 수 (면적)
cnt += half * half * N	N개의 사분면을 건너뛴 칸 수 누적

import java.io.*;
import java.util.*;

public class Main {
    static int n, r, c;
    static int cnt = 0;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        StringTokenizer st = new StringTokenizer(br.readLine());
        n = Integer.parseInt(st.nextToken());
        r = Integer.parseInt(st.nextToken()); // 찾고싶은 행
        c = Integer.parseInt(st.nextToken()); // 찾고싶은 열

        int size = (int) Math.pow(2, n); // 한 변의 길이
        Z(0, 0, size);
        System.out.println(cnt);
    }

    public static void Z(int x, int y, int size) {
        // size=1이면 더 이상 쪼갤 수 없음
        if (size == 1) {
            return;
        }

        // x, y: 현재 정사각형(사분면)의 좌상단 좌표
        // half: 현재 정사각형(사분면)의 한 변의 절반
        int half = size / 2;

        // 1사분면
        if (r < x + half && c < y + half) {
            Z(x, y, half);
        }
        // 2사분면
        else if (r < x + half && c >= y + half) {
            // 2사분면 (앞에 1사분면 1개 건너뜀 → 시작번호: 1 * half²)
            cnt += half * half;
            Z(x, y + half, half);
        }
        // 3사분면 (앞에 1,2사분면 2개 건너뜀 → 시작번호: 2 * half²)
        else if (r >= x + half && c < y + half) {
            cnt += half * half * 2;
            Z(x + half, y, half);
        }
        // 4사분면 (앞에 1~3사분면 3개 건너뜀 → 시작번호: 3 * half²)
        else {
            cnt += half * half * 3;
            Z(x + half, y + half, half);
        }
    }
}

반복문 (시간 초과)

import java.io.*;
import java.util.*;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        StringTokenizer st = new StringTokenizer(br.readLine());
        int n = Integer.parseInt(st.nextToken());
        int r = Integer.parseInt(st.nextToken());
        int c = Integer.parseInt(st.nextToken());

        int cnt = 0;
        int size = (int) Math.pow(2, n);

        int x = 0, y = 0;

        while (size > 1) {
            int half = size / 2;

            // 사분면 판별
            if (r < x + half && c < y + half) {
                // 1사분면: cnt += 0
            } else if (r < x + half && c >= y + half) {
                cnt += half * half;
                y += half; // 오른쪽 위로 이동
            } else if (r >= x + half && c < y + half) {
                cnt += half * half * 2;
                x += half; // 왼쪽 아래로 이동
            } else {
                cnt += half * half * 3;
                x += half;
                y += half; // 오른쪽 아래로 이동
            }

            size = half; // 더 작은 정사각형으로 이동
        }

        System.out.println(cnt);
    }
}