[Algorithm/Java] 백준 11727번 - 2×n 타일링 2

---

https://www.acmicpc.net/problem/11726

---

📌 문제

문제 유형

• DP

문제 설명

2×n 직사각형을 1×2, 2×1과 2×2 타일로 채우는 방법의 수를 구하는 프로그램을 작성하시오.

아래 그림은 2×17 직사각형을 채운 한가지 예이다.

입출력 예시

첫째 줄에 2×n 크기의 직사각형을 채우는 방법의 수를 10,007로 나눈 나머지를 출력한다. (1 ≤ n ≤ 1,000)

• 입력

  9
  

• 출력

  55
  

🔍 문제 풀이

아래는 n = 1부터 n = 3까지 가능한 타일링 경우를 시각적으로 정리한 것이다.

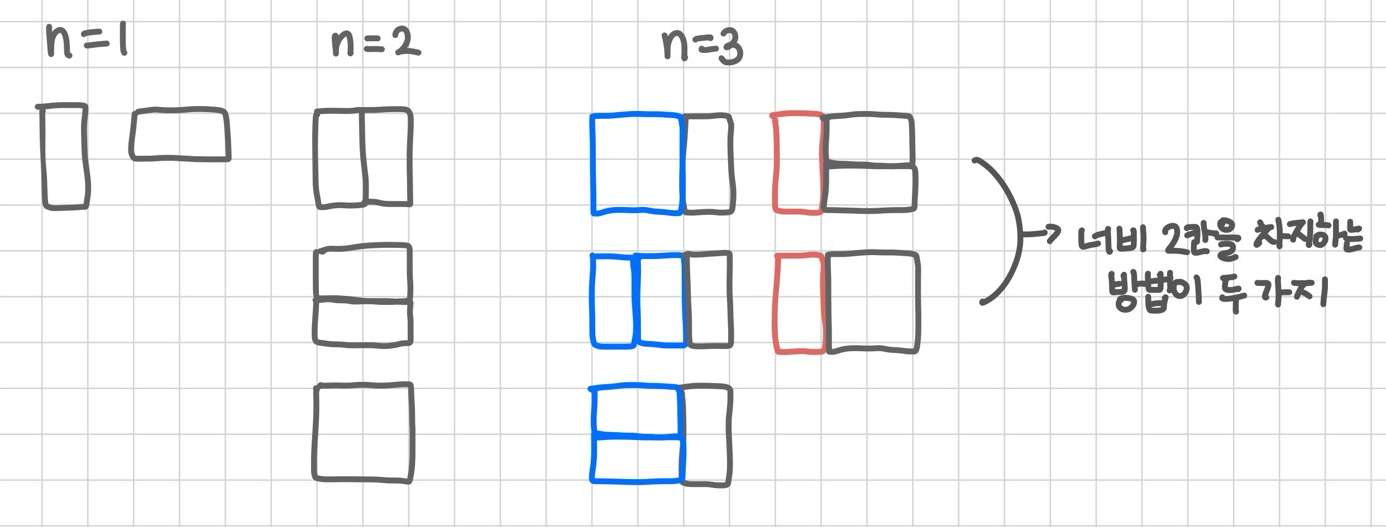
마지막 타일을 어떻게 놓느냐에 따라 점화식을 세울 수 있다:

• 세로 타일(2×1) 하나를 끝에 놓는 경우 → 남은 너비는 n - 1

  ⬜⬜⬜🟥    >    ⬜⬜⬜
  ⬜⬜⬜🟥    >    ⬜⬜⬜
  

• 가로 타일(1×2) 2개 또는 정사각형 타일(2×2) 을 붙이는 경우 → 남은 너비는 n - 2

  ⬜⬜🟥🟥    >    ⬜⬜        (가로 타일 2개)
  ⬜⬜🟥🟥    >    ⬜⬜
  
  ⬜⬜🟦🟦    >    ⬜⬜        (정사각형 타일 1개)
  ⬜⬜🟦🟦    >    ⬜⬜
  

이처럼 n-2인 경우에는 2가지 방식이 존재하므로, 점화식은 다음과 같다

dp[n] = dp[n - 1] + 2 * dp[n - 2];

💻 전체 코드

import java.io.*;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        int n = Integer.parseInt(br.readLine());
        int[] dp = new int[1001];
        dp[1] = 1;
        dp[2] = 3;

        for(int i=3; i<=n; i++){
            dp[i] = (dp[i-1]  + 2* dp[i-2] ) % 10007;
        }

        System.out.println(dp[n]);
    }
}