[Algorithm/Java] 백준 14500번 - 테트로미노 🧩
https://www.acmicpc.net/problem/14500
🔍 문제 풀이
문제 도식화
- DFS로 연속된 4칸을 탐색하며 최대값을 찾는다.
- DFS로 만들 수 없는 ㅗ, ㅏ, ㅜ, ㅓ 모양은 별도로 시뮬레이션 처리를 하여 최대값을 찾는다.
- ‘ㅗ’ 모양은 중심점에서 세 방향으로 뻗는 구조
- DFS로는 깊이 4까지 가는 도중 가지 하나가 끊기게 되므로 별도 처리 필요

알고리즘 선택
이 문제에서는 모든 칸에서 시작해, 상하좌우로 4칸을 탐색해야 하므로 DFS(깊이 우선 탐색) + 백트래킹이 가장 적합하다.
-
DFS (깊이 우선 탐색)
- 한 방향으로 끝까지 들어간 뒤, 막히면 뒤로 돌아오는 방식 (Backtracking)
- 재귀 기반 -> 백트래킹 가능
-
BFS (너비 우선 탐색)
- 현재에서 가까운 모든 위치를 먼저 탐색
- 큐 기반 -> 레벨 단위 탐색 -> 중간 분기 어려움
아래 그림은 DFS와 BFS가 탐색하는 순서를 비교한 것이다.
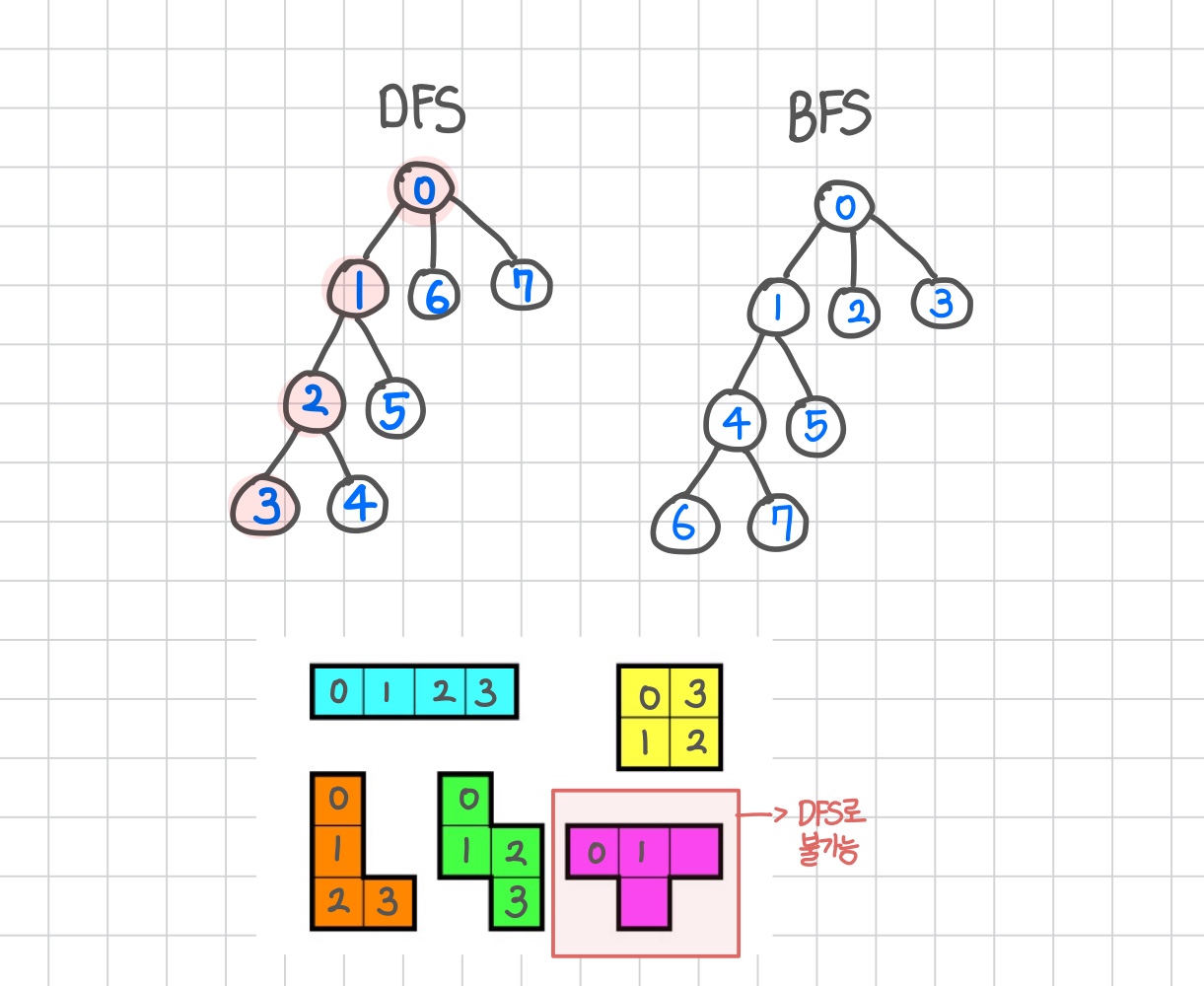
위 그림을 통해 BFS는 가능하긴 하나, 큐 상태에서 깊이 추적이 어렵다는 것을 확인할 수 있다.
따라서 가까운 칸부터 넓게 탐색하는 BFS보다, 한 방향으로 깊게 탐색하는 DFS가 더 적합하다.
단, ‘ㅗ’, ‘ㅜ’, ‘ㅏ’, ‘ㅓ’ 모양 도형은 DFS로 만들 수 없다.
- DFS는 한 방향으로만 계속 탐색하기 때문에, 중간에서 양쪽으로 분기하는(3방향으로 퍼지는) 구조를 만들 수 없다.
- 그럼 어떻게 처리해야할까? 알아보자.
‘ㅗ’모양은 어떻게 처리하지?
‘ㅗ’, ‘ㅏ’, ‘ㅜ’, ‘ㅓ’ 모양 도형은 상하좌우 탐색으로는 불가능하다.
따라서 checkTShape(x, y) 함수를 통해 현재 좌표 (x, y)를 중심으로 3방향을 더해 ㅗ 모양 도형을 만들 수 있도록 해줬다.
| 방향 | 좌표 변화 |
|---|---|
| 왼쪽 | x, y - 1 |
| 오른쪽 | x, y + 1 |
| 위쪽 | x - 1, y |
| 아래쪽 | x + 1, y |
int[][] Tshapes = {
{0, -1, -1, 0, 0, 1}, // ㅗ
{-1, 0, 0, 1, 1, 0}, // ㅏ
{0, -1, -1, 0, 1, 0}, // ㅓ
{0, -1, 0, 1, -1, 0} // ㅜ
};
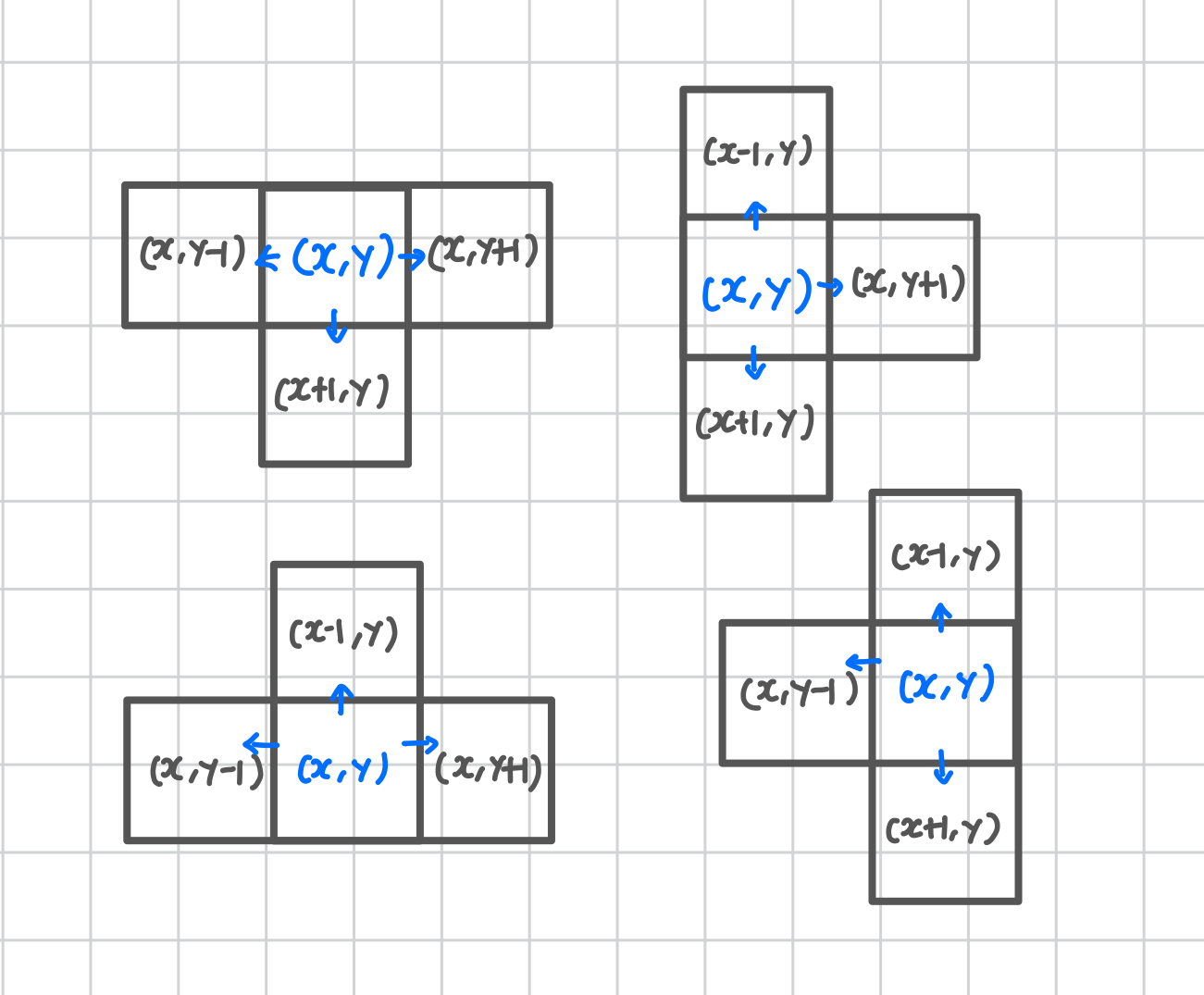
- 이처럼, 중심 좌표
(x, y)를 기준으로 양 방향으로 뻗어나가도록 해야 한다. - 즉, 중심 좌표를 기준으로 3개의 방향으로 확장하여 총 4칸을 구성하는 방식이다.
예를 들어 ㅗ 모양의 경우:
- 중심:
(x, y) - 확장: 왼쪽
(x, y - 1), 오른쪽(x, y + 1), 아래(x + 1, y)
이러한 방식으로 ㅏ, ㅓ, ㅜ, ㅗ 총 4가지 모양을 구현할 수 있다.
이처럼 모든 칸에서 모든 방향의 도형을 직접 시도하여 누적 최대값을 찾는다.
‘ㅗ’모양을처리하는 두 가지 방법
배열 반복 방식
- dx1 dy1, dx2 dy2, dx3 dy3 형태로 3개의 날개 좌표를 한 줄의 배열로 나열해서 처리한다.
- 중심 좌표 (x, y)를 기준으로 3개의 방향만 더해주기 때문에 간결하다.
- 도형 한 묶음을 검사하다가 실패하면 그 도형만 건너뛰어야 하므로
continue사용(도형별 검사)
public static void Tshape(int x, int y) {
// 중심(x, y) 기준 상대 좌표: 3개 날개
int[][] cases = {
{ 0, -1, -1, 0, 0, 1 }, // ㅗ
{ -1, 0, 0, 1, 1, 0 }, // ㅏ
{ 0, -1, 1, 0, 0, 1 }, // ㅜ
{ -1, 0, 0, -1, 1, 0 } // ㅓ
};
for (int[] c : cases) {
int nx1 = x + c[0], ny1 = y + c[1];
int nx2 = x + c[2], ny2 = y + c[3];
int nx3 = x + c[4], ny3 = y + c[5];
if (nx1 < 0 || nx1 >= n || ny1 < 0 || ny1 >= m) continue;
if (nx2 < 0 || nx2 >= n || ny2 < 0 || ny2 >= m) continue;
if (nx3 < 0 || nx3 >= n || ny3 < 0 || ny3 >= m) continue;
int sum = paper[x][y]
+ paper[nx1][ny1]
+ paper[nx2][ny2]
+ paper[nx3][ny3];
maxSum = Math.max(maxSum, sum);
}
}
좌표 분리 방식
- 4개의 좌표 쌍을 각각
{ {0,0}, {0,-1}, {0,1}, {-1,0} }처럼 배열로 분리하여 표현한다. - 반복문에서 바로 nx, ny를 계산하여 합산할 수 있어 편리하다.
- 좌표 하나씩 검사하다가 실패하면 그 도형 전체 중단해야 하므로
break + isValid사용 (좌표별 검사)
public static void Tshape(int x, int y) {
int[][][] shapes = {
{ {0, 0}, {0, -1}, {-1, 0}, {0, 1} }, // ㅗ
{ {0, 0}, {-1, 0}, {0, 1}, {1, 0} }, // ㅏ
{ {0, 0}, {0, -1}, {1, 0}, {0, 1} }, // ㅜ
{ {0, 0}, {-1, 0}, {0, -1}, {1, 0} } // ㅓ
};
for (int[][] shape : shapes) { // 하나의 도형
int sum = 0;
boolean isValid = true;
for (int[] d : shape) { // 각 도형의 날개 묶음
int nx = x + d[0];
int ny = y + d[1];
if (nx < 0 || nx >= n || ny < 0 || ny >= m) {
isValid = false;
break;
}
sum += paper[nx][ny];
}
if (isValid) maxSum = Math.max(maxSum, sum);
}
}
💥 메모리를 줄여보자
테트로미노 문제를 풀었을 때, 정답은 맞췄지만 메모리 사용량이 무려 283080KB가 나와서 깜짝 놀랐다.
다른 사람들은 보통 3~8만 KB 정도였는데, 나는 왜 이렇게 많이 나왔을까?
원인 분석
처음에는 dfs() 함수 안에 다음과 같은 방향 벡터를 매번 선언했다.
public void dfs(...) {
int[] dx = {-1, 1, 0, 0};
int[] dy = {0, 0, -1, 1};
}
- 이 코드는 DFS가 호출될 때마다 새로운
int[]배열을 생성한다. - 테트로미노 문제에서는 DFS가 수만 번 이상 호출되므로 결과적으로
int[]객체 수천~수만 개가 힙에 쌓이게 된다. - 이게 JVM 메모리 폭증의 주범이었다.
해결
문제의 방향 벡터를 함수 내부에서 선언하지 않고,
전역으로 빼주기만 해도 메모리 사용량이 눈에 띄게 줄어든다.
이렇게 고정된 배열은 한 번만 생성되고 모든 DFS 호출에서 재사용되기 때문에
힙 메모리 누적을 방지할 수 있다.
static int[] dx = {-1, 1, 0, 0};
static int[] dy = {0, 0, -1, 1};
확실히 개선된 것을 알 수 있다.

💻 전체 코드
import java.io.*;
import java.util.*;
public class Main {
static int[][] paper;
static boolean[][] visited;
static int n, m;
static int maxSum = 0;
static int[] dx = {-1, 1, 0, 0};
static int[] dy = {0, 0, -1, 1};
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
// 입력
StringTokenizer st = new StringTokenizer(br.readLine());
n = Integer.parseInt(st.nextToken()); // 행
m = Integer.parseInt(st.nextToken()); // 열
paper = new int[n][m];
visited = new boolean[n][m];
// 초기화
for(int i = 0; i < n; i++){
st = new StringTokenizer(br.readLine());
for(int j = 0; j < m ; j++){
paper[i][j] = Integer.parseInt(st.nextToken());
}
}
// buildBlock, Tshape 호출
for(int i = 0; i < n; i++){
for(int j = 0; j< m ; j++){
visited[i][j] = true;
// i,j 현재 블록의 좌표 (시작점이자 첫 번째 칸)
// depth=1부터 시작(시작 좌표 포함),
buildBlock(i, j, 1, paper[i][j]); // 시작 좌표에서 DFS 시작
visited[i][j] = false; // 시작점 탐색 후 백트래킹
Tshape(i, j);
}
}
System.out.println(maxSum);
}
// 연속된 4칸 블록 놓기 (ㅗ 모양 제외)
public static void buildBlock(int x, int y, int depth, int total) {
if (depth == 4) {
maxSum = Math.max(maxSum, total);
return;
}
// 상하좌우로만 이동 가능
for (int i = 0; i < 4; i++) {
int nx = x + dx[i];
int ny = y + dy[i];
if(nx < 0 || nx >= n || ny < 0 || ny >= m) continue;
if (!visited[nx][ny]) {
visited[nx][ny] = true;
buildBlock(nx, ny, depth + 1, total + paper[nx][ny]);
visited[nx][ny] = false; // 새로운 경로 탐색 후 백트래킹
}
}
}
// ㅗ 모양 탐색
public static void Tshape(int x, int y){
// 방향백터 정의
int[][] cases = {
// dx1 dy1 dx2 dy2 dx3 dy3 (중심(x,y) 기준 3칸의 상대 좌표)
{ 0, -1, -1, 0, 0, 1 }, // ㅗ
{ -1, 0, 0, 1, 1, 0 }, // ㅏ
{ 0, -1, 1, 0, 0, 1 }, // ㅜ
{ -1, 0, 0, -1, 1, 0 } // ㅓ
};
int sum = 0;
for(int[] c : cases){
// 한 모양에 대한 양쪽 3개 날개
int nx1 = x + c[0], ny1 = y + c[1];
int nx2 = x + c[2], ny2 = y + c[3];
int nx3 = x + c[4], ny3 = y + c[5];
if(nx1 < 0 || nx1 >= n || ny1 < 0 || ny1 >= m) continue;
if(nx2 < 0 || nx2 >= n || ny2 < 0 || ny2 >= m) continue;
if(nx3 < 0 || nx3 >= n || ny3 < 0 || ny3 >= m) continue;
sum = paper[x][y] + paper[nx1][ny1] + paper[nx2][ny2] + paper[nx3][ny3];
maxSum = Math.max(maxSum, sum);
}
}
}
이로써 class 3 문제 해결 완료! 🤗

댓글남기기