[Algorithm/Java] 백준 15829번 - Hashing

---

https://www.acmicpc.net/problem/15829

---

📌 문제

문제 유형

• 구현
• 문자열
• 해싱

문제 설명

• 문자열은 영문 소문자(a~z)로만 구성
• 각 문자는 숫자로 변환: a=1, b=2, …, z=26
• 변환된 값에 고유한 가중치 r^i를 곱하고 모두 더함
• 최종 결과를 M = 1234567891로 나눈 나머지를 출력

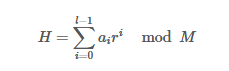
H = (a₁ × r⁰ + a₂ × r¹ + a₃ × r² + ... + aₙ × rⁿ⁻¹) mod M

• aᵢ: i번째 문자의 숫자값 (a=1, b=2, …, z=26)
• r: 31
• M: 1234567891

입출력 예시

입력

5
abcde

출력

4739715

🔍 문제 풀이

❌ 처음 짠 코드 (50점)

• Math.pow()는 double을 반환하여 정밀도 손실이 발생할 수 있음
• % 1234567891 처리를 하지 않아 오버플로우 발생 가능

import java.io.*;
import java.util.*;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        int L = Integer.parseInt(br.readLine());
        String str = br.readLine();

        int result = 0;
        for (int i = 0; i < L; i++) {
            char chr = str.charAt(i);
            int temp = chr - 'a' + 1;

            result += temp * Math.pow(31, i);
        }
        System.out.println(result);
    }
}

• Java에서 int는 최대 약 21억 (2³¹ - 1), long은 최대 약 9.2경 (2⁶³ - 1)
• 하지만 31^i는 지수 함수이기 때문에 매우 빠르게 커짐
• e.g., 31^25 ≈ 8.2 × 10³⁷ → 이미 long 범위를 초과함

따라서 % M 없이 계산하면 오버플로우로 인해
결과에 이상한 값이 들어가게 됨

모듈러 연산의 성질 을 활용하면,

연산 도중에도 나머지를 취해도 결과가 같기 때문에, 매 연산마다 % M을 적용해도 최종 결과에는 영향이 없으며,

계산 도중 값이 너무 커져서 오버플로우가 발생하는 것도 방지할 수 있다.

(a + b) % M = (a % M + b % M) % M
(a × b) % M = (a % M × b % M) % M

✅ 수정한 코드 (100점)

• r = 31^i를 직접 곱해가며 구함 (Math.pow 제거)
• 매 연산마다 % M 적용하여 오버플로우 방지

⚠️ 처음에는 result += (temp * ...) 방식으로만 누적하고, 마지막에 한 번만 % M 연산을 적용했는데, 이렇게 하면 중간 계산 값이 매우 커지면서 오버플로우가 발생할 수 있다.

package org.example;

import java.io.*;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        int L = Integer.parseInt(br.readLine());
        String str = br.readLine();
        long r = 1;
        int M = 1234567891;

        long result = 0;
        for (int i = 0; i < L; i++) {
            long temp = str.charAt(i) - 'a' + 1;
            result = (result + temp * r) % M;
            r = (r * 31) % M;
        }

        System.out.println(result);
    }
}

💭 배운 점

• 해시 함수를 구현할 때 Math.pow()를 쓰면 안 된다.
  • 정수 오차 없이 계산하려면 반복문으로 직접 거듭제곱을 누적해야 함
• 모듈러 연산(% M)은 매 연산마다 해줘야 한다.
  • 중간 결과가 int/long 범위를 넘지 않도록 하는 것이며, 문제에서 요구한 해시값 포맷을 지키는 방법이다.