[Algorithm/Java] 백준 1932번 - 정수 삼각형

---

https://www.acmicpc.net/problem/1932

---

📌 문제

문제 유형

• DP

📘 문제 설명

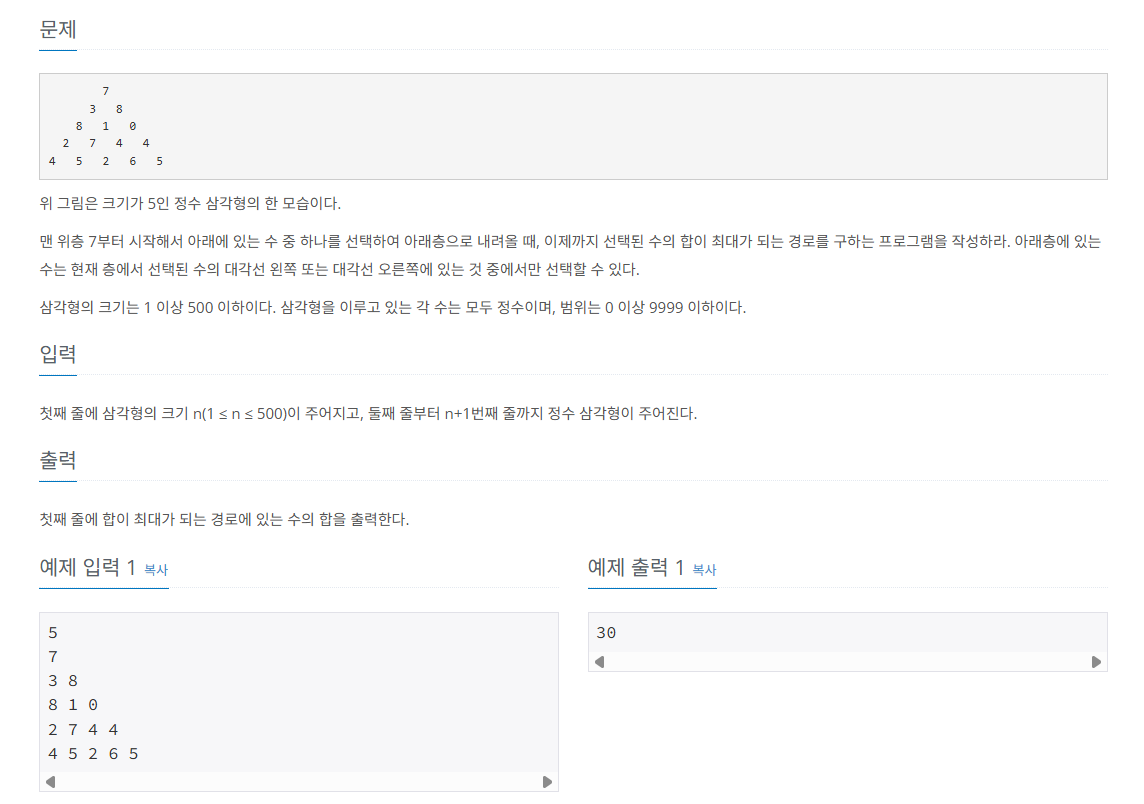
🔍 문제 풀이

문제 해결 절차

이 문제는 반복문 Bottom-Up 방식(상향식)의 전형적인 DP 문제이다.

DFS + 메모이제이션을 활용한 Top-Down 풀이도 가능하지만, 구현이 간단한 Bottom-Up 방식으로 풀었다.

1. 삼각형의 각 가중치를 arr 배열에 저장한다.
2. 가장 아래 행(n-1)을 dp 배열에 복사한다.
   • 밑에서부터 위로 올라오면서 최댓값을 누적하는 구조
3. n-2행부터 0행까지 다음 점화식으로 계산한다.
4. 최종적으로 dp[0][0]에는 전체 경로 중 최대 합이 저장된다.

점화식

dp[i][j] = Math.max(dp[i+1][j], dp[i+1][j+1]) + arr[i][j];

💻 전체 코드

DP (Bottom-Up)

import java.io.*;
import java.util.*;

public class Main {
    public static void main (String[]args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        int n = Integer.parseInt(br.readLine());
        int[][] arr = new int[n][n];
        int[][] dp = new int[n][n];


        // arr 배열 초기화
        for(int i=0; i<n; i++){
            StringTokenizer st = new StringTokenizer(br.readLine());
            for(int j=0; j<=i; j++){
                arr[i][j] = Integer.parseInt(st.nextToken());
            }
        }

        // 맨 아래 행 dp 배열에 복사
        for(int i=0; i<n; i++){
            dp[n-1][i] = arr[n-1][i];
        }

        // dp계산
        for (int i = n-2; i >= 0; i--) {
            for (int j = 0; j <= i; j++) {
                dp[i][j] = Math.max(dp[i+1][j], dp[i+1][j+1]) + arr[i][j];
            }
        }

        // 꼭대기 출력
        System.out.println(dp[0][0]);
    }
}

DFS (Top-Down)

import java.io.*;
import java.util.*;

public class Main {
    static int[][] arr;
    static int[][] dp;
    static int n;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        n = Integer.parseInt(br.readLine());
        arr = new int[n][n];
        dp = new int[n][n];

        for (int i = 0; i < n; i++) {
            Arrays.fill(dp[i], -1);  // -1로 초기화 (아직 계산 안 됐다는 뜻)
            StringTokenizer st = new StringTokenizer(br.readLine());
            for (int j = 0; j <= i; j++) {
                arr[i][j] = Integer.parseInt(st.nextToken());
            }
        }

        System.out.println(dfs(0, 0));  // 꼭대기부터 시작
    }

    public static int dfs(int x, int y) {
        // 범위 끝에 도달한 경우
        if (x == n - 1) return arr[x][y];

        // 이미 계산된 값이면 반환
        if (dp[x][y] != -1) return dp[x][y];

        // 아래 두 경로 중 큰 값 + 현재 값
        int left = dfs(x + 1, y);
        int right = dfs(x + 1, y + 1);

        return dp[x][y] = Math.max(left, right) + arr[x][y];
    }
}