[Algorithm/Java] 백준 1991번 - 트리 순회

---

https://www.acmicpc.net/problem/1991

---

📌 문제

문제 유형

• 트리
• 재귀

📘 문제 설명

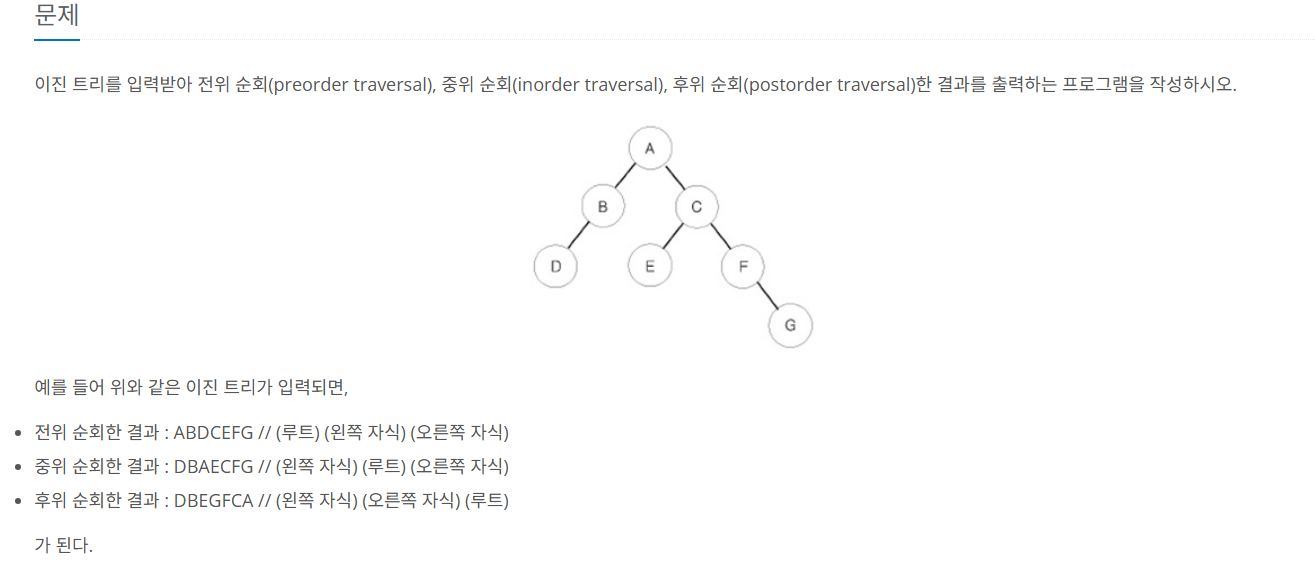
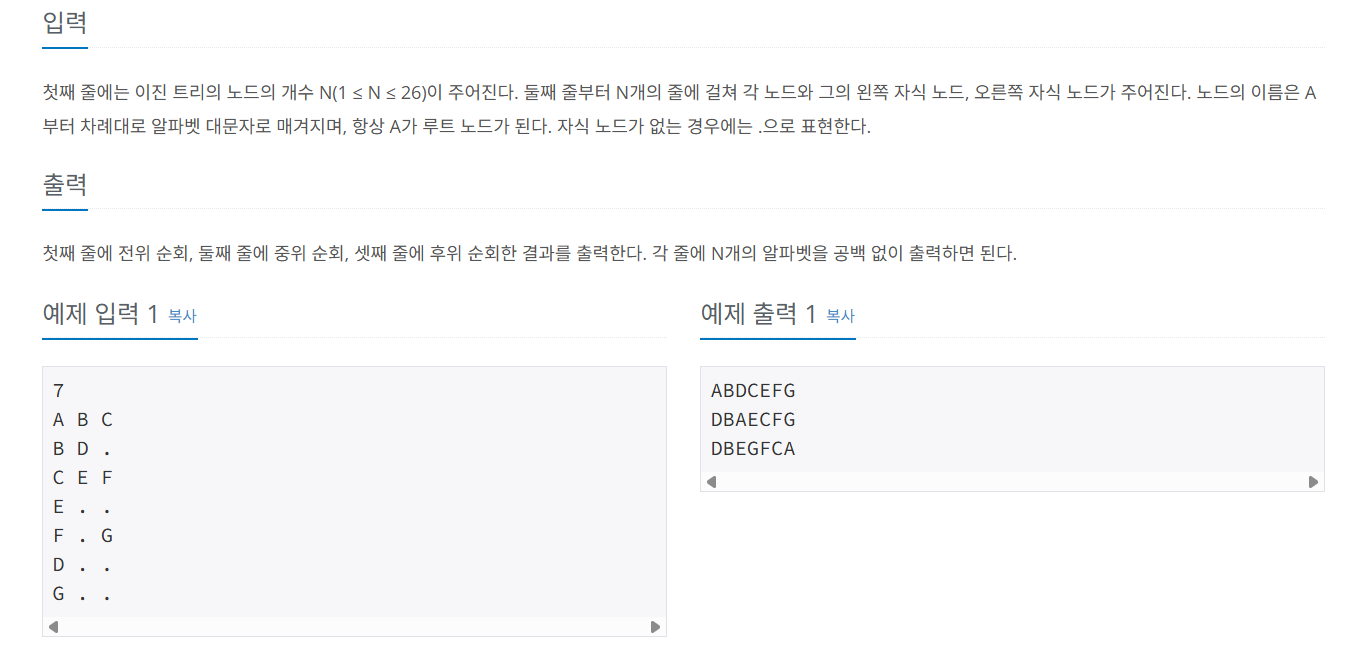
🔍 문제 풀이

문제 해결 절차

1. Node 클래스로 트리의 한 정점 표현
   • 값과 자식 노드를 함께 저장하기 위해 클래스 사용
   • Node 클래스는 트리의 한 정점을 나타내며, value, left, right 필드를 가짐
   • 트리 구조는 처음부터 자식 노드를 알고 있는 게 아니라, 입력을 통해 나중에 연결하므로, 생성자에서는 value만 초기화해야함
   • left와 right는 이후 입력 정보를 통해 필요할 때 연결
     
     
2. 알파벳 문자(A~Z)를 배열 인덱스로 변환해 Node[]에 미리 노드 생성
   
   
3. 입력 받은 부모-자식 관계를 통해 트리 연결
   • tree[root - 'A']를 기준으로, 해당 노드의 left와 right를 연결
   • 만약 입력 값이 .이라면 자식이 없다는 뜻이므로 연결 생략
     
     
4. 루트 노드 tree[0] (A노드)부터 전위/중위/후위 순회 시작

Node 클래스 정리

Node는 내가 만든 클래스(사용자 정의 자료형)이다.

• 자바에서는 클래스명이 곧 자료형처럼 사용된다.
• Node left;는 Node 타입 객체를 가리키는 변수이다.
• 이를 통해 노드 간 연결이 가능해지고, 트리 구조를 만들 수 있다.

사용 예시

Node a = new Node();
a.value = 'A';

Node b = new Node();
b.value = 'B';

a.left = b; // A의 왼쪽 자식이 B

결과: a -> b로 연결된 트리의 일부

예시

예를 들어 입력이 아래와 같을 때

A B C
B D .
C E F
D . .
E . .
F . .

아래와 같이 각 줄이 처리된다.

// A B C
tree[0].left  = tree[1];  // A → B
tree[0].right = tree[2];  // A → C

// B D .
tree[1].left  = tree[3];  // B → D
// 오른쪽은 '.' → 연결 생략

// C E F
tree[2].left  = tree[4];  // C → E
tree[2].right = tree[5];  // C → F

// D, E, F는 모두 자식 없음 -> 연결 생략

트리 도식화

        A
      /   \
     B     C
    /     / \
   D     E   F

tree 배열 인덱스 상태

인덱스	value	left	right
0	‘A’	‘B’	‘C’
1	‘B’	‘D’	null
2	‘C’	‘E’	‘F’
3	‘D’	null	null
4	‘E’	null	null
5	‘F’	null	null

위 트리 구조에 대한 전위 / 중위 / 후위 순회 결과는 아래와 같다.

전위 순회:    A → B → D → C → E → F   → ABDCEF
중위 순회:    D → B → A → E → C → F   → DBAECF
후위 순회:    D → B → E → F → C → A   → DBEFCA

💻 전체 코드

import java.io.*;
import java.util.*;

public class Main {
    // 트리 노드 정보 클래스 생성
    static class Node {
        char value;
        Node left;
        Node right;

        Node(char value) {
            this.value = value;
        }
    }

    static Node[] tree = new Node[26];
    static StringBuilder sb = new StringBuilder();

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int n = Integer.parseInt(br.readLine());

        // 트리 노드 초기화
        for (int i=0; i<26; i++) {
            tree[i] = new Node((char) ('A' + i));
        }

        // 노드 연결 정보 입력
        for (int i=0; i<n; i++) {
            StringTokenizer st = new StringTokenizer(br.readLine());
            char root = st.nextToken().charAt(0);
            char left = st.nextToken().charAt(0);
            char right = st.nextToken().charAt(0);

            if (left != '.') {
                tree[root - 'A'].left = tree[left - 'A'];  // 문자를 인덱스로 변환
            }
            if (right != '.') {
                tree[root - 'A'].right = tree[right - 'A'];
            }
        }

        // // 디버깅
        // Node root = tree[0];
        // System.out.println("root: " + root.val); // A
        // System.out.println("left: " + (root.left != null ? root.left.val : "null")); // B
        // System.out.println("right: " + (root.right != null ? root.right.val : "null")); // C

        // 순회 시작 (루트는 `A`)
        preorder(tree[0]); // = preorder(new Node('A'))
        sb.append('\n');

        inorder(tree[0]);
        sb.append('\n');

        postorder(tree[0]);
        System.out.println(sb);
    }

    // 전위 (루트 -> 왼쪽 -> 오른쪽)
    static void preorder(Node node) {
        if (node == null) return;
        sb.append(node.value);
        preorder(node.left);
        preorder(node.right);
    }

    // 중위 (왼쪽 -> 루트 -> 오른쪽)
    static void inorder(Node node) {
        if (node == null) return;
        inorder(node.left);
        sb.append(node.value);
        inorder(node.right);
    }

    // 후위 (왼쪽 -> 오른쪽 -> 루트)
    static void postorder(Node node) {
        if (node == null) return;
        postorder(node.left);
        postorder(node.right);
        sb.append(node.value);
    }
}