[Algorithm/Java] SWEA 5102 - 노드의 거리

---

SWEA 5102 - 노드의 거리

---

🔍 문제 풀이

문제 도식화

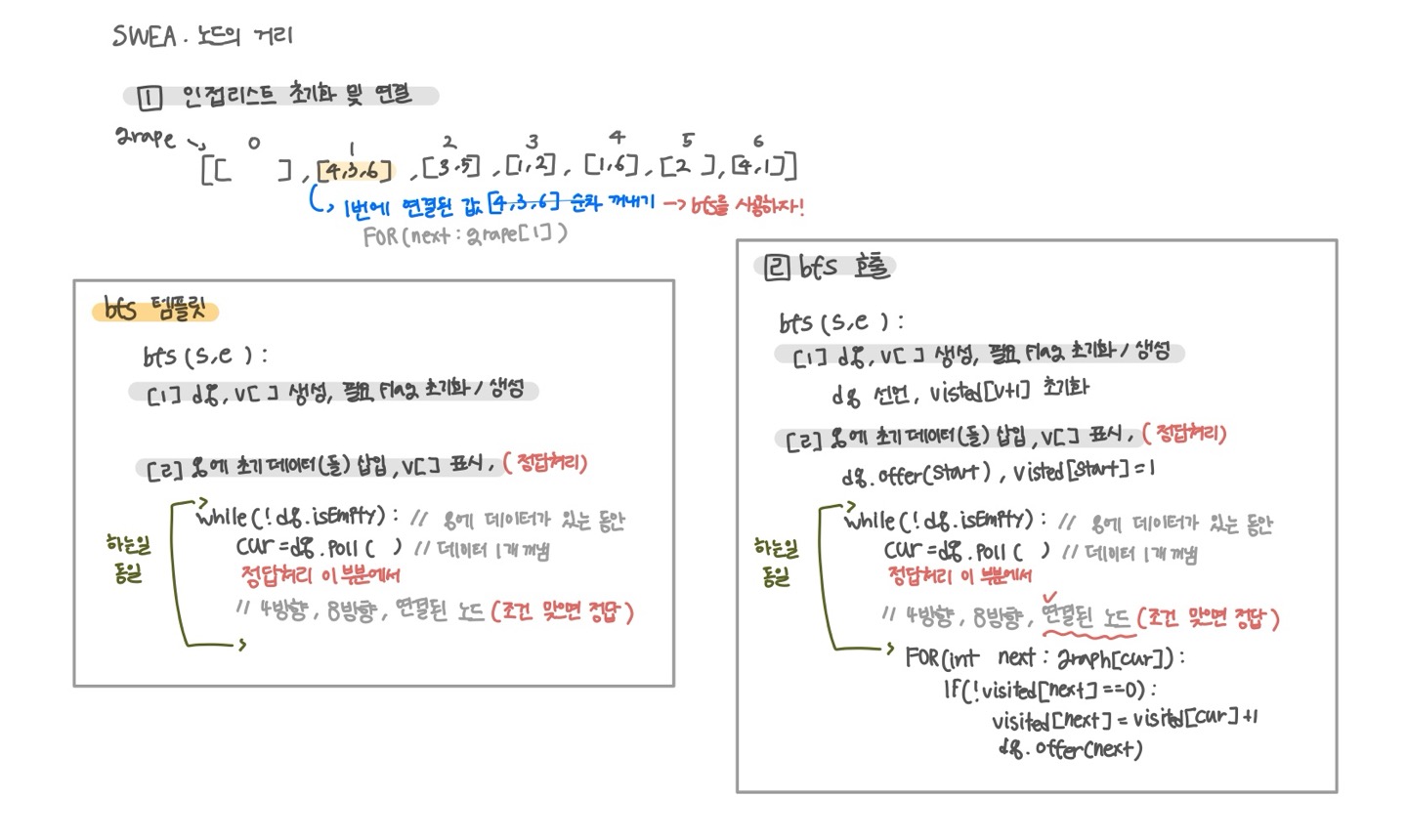
인접 행렬 vs 인접 리스트

인접 행렬

모든 노드 쌍 정보를 저장, 연결 안 되면 0, 연결되면 1

2차원 배열로 구현 int[v+1][v+1]

• 장점: 두 노드 연결 여부 확인 O(1)
• 단점: 메모리 낭비, 탐색 시 불필요한 0도 확인해야 함

   1  2  3
1 [0, 1, 1]
2 [1, 0, 0]
3 [1, 0, 0]

graph = new int[v + 1][v + 1]; // 인접 행렬

// 간선 입력 (무방향)
for (int i = 0; i < e; i++) {
    st = new StringTokenizer(br.readLine());
    int a = Integer.parseInt(st.nextToken());
    int b = Integer.parseInt(st.nextToken());
    graph[a][b] = 1;
    graph[b][a] = 1;
}

인접 리스트

연결된 노드만 저장

List<Integer>[] graph 로 구현

• 바깥쪽은 배열 (n+1칸 고정)
• 안쪽은 리스트 (칸마다 크기 가변)
  • 장점: 메모리 효율적, 연결된 애들만 순회
  • 단점: 두 노드 연결 여부 확인 시 O(차수)

graph[1] = [2, 3]
graph[2] = [1]
graph[3] = [1]

graph = new ArrayList[v + 1]; // 인접 리스트

// ArrayList를 담을 수 있는 공간만 만들어 두는 거고, 각 칸에는 아직 null이 들어있음
for (int i = 1; i <= v; i++) {
    graph[i] = new ArrayList<>(); // [null, [], [], []]
}

// 간선 입력 (무방향)
for (int i = 0; i < e; i++) {
    st = new StringTokenizer(br.readLine());
    int a = Integer.parseInt(st.nextToken());
    int b = Integer.parseInt(st.nextToken());
    graph[a].add(b);
    graph[b].add(a);
}

💻 코드

전체 코드

import java.io.*;
import java.util.*;

public class Solution {
    static List<Integer>[] graph;
    static int[] visited;
    static int v, e;

    public static void main(String[] args) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringBuilder sb = new StringBuilder();
        int T = Integer.parseInt(br.readLine());

        for (int tc = 1; tc <= T; tc++) {
            StringTokenizer st = new StringTokenizer(br.readLine());
            v = Integer.parseInt(st.nextToken());
            e = Integer.parseInt(st.nextToken());

            // 인접 리스트 초기화
            graph = new ArrayList[v + 1];
            for (int i = 1; i <= v; i++) graph[i] = new ArrayList<>();

            // 인접 리스트 연결 (무방향)
            for (int i = 0; i < e; i++) {
                st = new StringTokenizer(br.readLine());
                int a = Integer.parseInt(st.nextToken());
                int b = Integer.parseInt(st.nextToken());
                graph[a].add(b);
                graph[b].add(a);
            }

            // 출발 노드, 도착 노드 입력
            st = new StringTokenizer(br.readLine());
            int start = Integer.parseInt(st.nextToken());
            int end = Integer.parseInt(st.nextToken());

            // dfs 실행 후 결과 출력
            int ans = bfs(start, end);
            sb.append('#').append(tc).append(' ').append(ans).append('\n');
        }
        System.out.print(sb);
    }

    static int bfs(int start, int end) {
        // [1] dq, v[] 생성 및 필요 변수 선언
        Deque<Integer> dq = new ArrayDeque<>();
        visited = new int[v + 1];

        // [2] dq에 초기 데이터들 삽입, v[] 표시
        dq.offer(start);
        visited[start] = 1; // 시작점 거리 = 1로 두고, 최종 답에서 -1 처리

        while (!dq.isEmpty()) { // dq에 데이터가 있는 동안
            int cur = dq.poll(); // 현재 노드 꺼내기

            if (cur == end) return visited[cur] - 1; // 정답 처리 (시작을 1로 했으니 -1 보정)

            // 현재 노드와 연결된 모든 노드 탐색
            for (int next : graph[cur]) { // 연결된 노드
                if (visited[next] == 0) { // 미방문 노드라면
                    // 위([2]]번과 똑같은 작업
                    dq.offer(next);
                    visited[next] = visited[cur] + 1;
                }
            }
        }

        // 목적지를 방문하지 못한 경우
        return 0;
    }
}

스켈레톤 코드

import java.io.*;
import java.util.*;

public class Solution {
    static List<Integer>[] graph;
    static int[] visited;
    static int v, e;

    public static void main(String[] args) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringBuilder sb = new StringBuilder();
        int T = Integer.parseInt(br.readLine());

        for (int tc = 1; tc <= T; tc++) {
            StringTokenizer st = new StringTokenizer(br.readLine());
            v = Integer.parseInt(st.nextToken());
            e = Integer.parseInt(st.nextToken());

            // 인접 리스트 또는 인접 행렬 연결 (무방향)



            st = new StringTokenizer(br.readLine());
            int start = Integer.parseInt(st.nextToken());
            int end = Integer.parseInt(st.nextToken());


            int ans = bfs(start, end);
            sb.append('#').append(tc).append(' ').append(ans).append('\n');
        }
        System.out.print(sb);
    }

    static int bfs(int start, int end) {



    }
}