[OS] #26 Main Memory
1. Main Memory
1.1 개요
프로세스는 실행 중인 프로그램을 말하는데, 여기서 “실행 중”이라는 말은 메인 메모리에 올라갔다는 뜻이다.
-
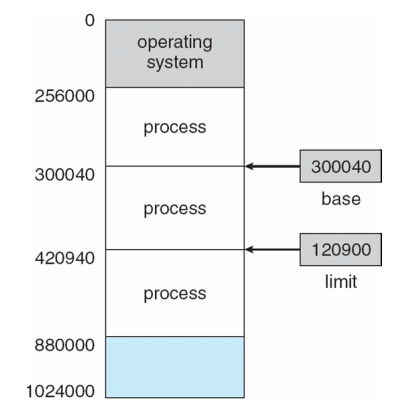
메모리 상단에는 OS(커널)가 존재하고 나머지 프로세스가 자신들의 메모리 공간을 사용하고 있다. 어떻게 서로의 메모리 공간을 침범하지 않고 보장해줄 수 있을까?
- 독립적인 메모리 공간을 위해 base register(기준 레지스터), limit register (한계 레지스터) 가 필요하다!
- CPU가 base보다 크고, base + limit보다 작은 범위 내의 주소에만 접근할 수 있도록 한다.
- base register: 프로세스의 물리적 메모리의 시작 주소를 가지고 있다.
- limit register: 현재 CPU에서 수행중인 프로세스의 논리적 주소의 최대값, 프로세스의 크기를 가지고 있다.
1.2 주소 바인딩
프로세스는 실행을 위해 메모리에 적재되면 프로세스를 위한 독자적인 주소공간이 생긴다. 이 주소를 논리적 주소라고 한다.
하지만 이 때 직접적인 주소 값을 받는 것이 아닌 논리적 주소를 할당 받게 되는데,
논리적 주소만으로는 실제 메모리의 주소를 알 수 없기 때문에 논리적 주소를 물리적(실제) 주소와 맵핑을 해주는 것을 메모리 주소 바인딩 이라고 한다.
왜 프로세스는 논리적 주소를 사용할까?
만약, 직접 주소를 각 프로세스에게 부여 하게 된다면 다른 프로세스가 점유하고 있는 메모리 공간에 접근했을 때 데이터가 훼손될 수도 있기 때문이다!
1.3 바인딩의 구분
메모리 주소 바인딩의 종류는 실제 주소와 논리적 주소를 연결하는 타이밍으로 구분하여 “컴파일”, “로드”, “실행 시간” 총 3가지로 구분된다.
현대 컴퓨터는 실행 타임 바인딩 방식을 사용한다.
실행 시간 바인딩 (Execution Time)
- 프로그램이 실행 이후에도, 프로그램이 위치한 물리적 메모리상의 주소가 변경될 수 있는 바인딩 방식이다.
- CPU가 주소를 참조할 때마다 해당 데이터가 물리적 메모리의 어느 위치에 존재하는지 주소 매핑 테이블을 이용해 주소 바인딩을 점검한다.
- 실행 시간 바인딩을 사용하기 위해 base register, limit register를 포함한 MMU와 같은 하드웨어를 이용한다.
- MMU는 좀 이따 살펴보자!
1.4 논리 주소 공간 vs 물리 주소 공간
논리 주소 (Logical address)
- CPU에 의해 만들어지며 가상의 주소
- CPU가 만드는 주소는 모두 논리 주소이다.
물리 주소 (Physical address)
- 저장공간에 실제로 존재하는 물리적 주소
1.5 MMU
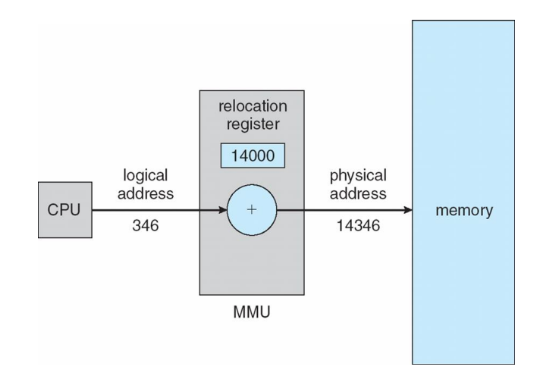
MMU(Memory Management Unit) : 실행 시간에 논리적 주소를 물리적 주소로 맵핑해주는 하드웨어
- 사용자 프로그램은 논리적 주소만 다루므로 MMU가 논리 주소를 물리 주소로 매핑해준다.
논리적 주소 + 베이스 레지스터를 함으로써 실제 주소를 찾아준다.
2. 메모리 배치 전략
2.1 단편화
외부 단편화
- 프로그램 크기보다 분할된 메모리 크기가 작아 프로세스를 수용하지 못하고 계속 낭비되는 공간이 발생하는 현상
- 가변 분할에서 발생한다. (너무 작은 hole들이 생김)
내부 단편화
- 분할된 메모리 보다 프로그램의 크기가 작아 분할된 메모리 내에 낭비되는 공간이 발생하는 현상
- 고정 분할에서 발생한다. (2002를 요구해야 하지만 분할 크기가 2000이라면 4000을 할당해야 함)
2.2 메모리 할당
2.2.1 불연속 / 연속 할당
불연속 할당
프로그램을 구성하는 주소 공간을 같은 크기의 페이지로 잘게 쪼개서 페이지 단위로 메모리에 올리는 방식
연속 할당
- 프로그램이 메모리에 올라갈 때 통째로 메모리에 올라가는 방식
- 고정 분할 방식, 가변 분할 방식이 존재한다.
2.2.2 고정 / 가변 분할 방식
고정 분할 방식
- 메모리 공간을 미리 분할하고 이 공간에 프로세스를 할당하는 방식이다.
- 내부 단편화가 발생할 수 있다.
-
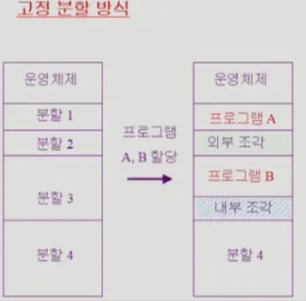
아래 그림은 분할 1 공간에 프로그램 A가 할당된 것을 볼 수 있고, 프로그램 B는 분할 2 공간에 크기 상 로드될 수 없어 좀 더 큰 공간인 분할 3에 할당된 상황이다.
가변 분할 방식
- 프로그램의 크기대로 메모리를 분할해서 할당하는 방식
- 외부 단편화가 발생할 수 있다.
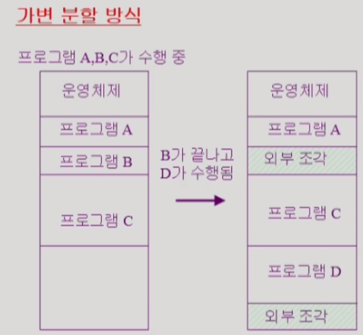
- 아래 그림은 프로그램 B가 끝난 공간이 할당되야 할 프로그램 D의 크기보다 작아 C밑에 할당되어 프로그램 B가 끝난 공간이 외부 조각이 된 상황이다.
2.3 Dynamic Storage-Allocation Problem
hole
가변 분할 방식을 사용하게 되면 프로그램이 실행되다가 종료가 되면 비어있는 메모리 공간인 hole이 생긴다.
Dynamic Storage-Allocation Problem
- 가변 분할 방식의 외부 단편화 문제를 해결하기 위한 메모리 배치 방식 문제
-
즉, 가장 적절한 hole을 찾는 문제이다❗
알고리즘 설명 First Fit (최초 배치) - 프로세스를 제일 먼저 발견한 hole에 배치.
- 빈 공간을 탐색하는 시간을 줄일 수 있지만 단편화를 고려하지 않음.Best Fit (최적 배치) - 메모리의 빈 공간을 모두 탐색 후, 프로세스의 크기보다 큰 hole 중 가장 작은 hole에 배치.
- 단편화의 크기를 줄일 수 있지만 탐색하는 시간이 필요하고, 아주 작은 hole들이 생겨 버려지는 단편화가 많아질 수 있음.Worst Fit (최악 배치) - 가장 큰 hole에 프로세스를 배치.
- 탐색 시간이 필요하고, 당장에 큰 단편화를 발생시켜 효율이 좋지 않음.
2.4 외부 단편화 문제 해결
Compaction, Coalescing은 연속 분할 할당에서 사용되는 외부 단편화 문제 해결 방법이다. (참고만 하자!)
- Compaction (메모리 압축)
- 불연속한 두 개 이상의 hole을 붙히는 것
- 즉, 메모리에 존재하는 여러 흩어진 단편화 영역 혹은 빈 영역들을 한곳으로 모아 큰 덩어리 (block)를 만드는 것
- 프로그램들의 재배치 필요
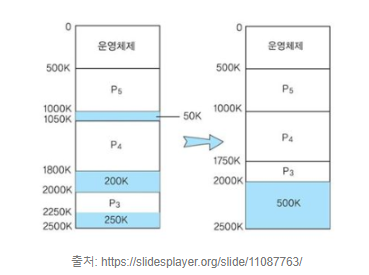
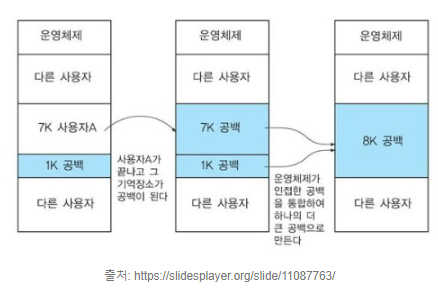
- Coalescing (메모리 통합)
- 연속한 두 개 이상의 hole을 합치는 것
- 즉, 인접한 단편화 영역 혹은 빈 영역들을 합침
- 프로그램 재배치 필요 X
3. 페이징
페이징 개념은 왜 이렇게 어려울까.. 시험 끝나고 나중에 꼭 다시 공부하자…🥹
3.1 페이징이란?
프로세스의 논리 주소의 메모리를 고정된 크기의 페이지(Page)라는 일정 단위로 자르고, 메모리의 논리 주소 공간을 프레임(frame)이라는 페이지와 동일 일정한 크기로 자른 뒤 페이지를 프레임에 할당하는 가상 메모리 관리 기법을 말한다.
모든 프로세스를 일정 크기로 자르고, 이를 메모리에 불연속적으로 할당하여 외부단편화를 해결한다.
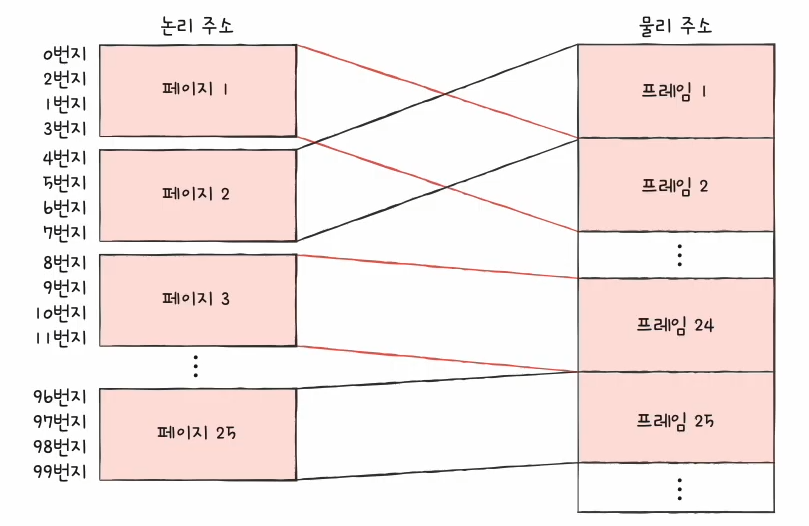
page와 frame은 메모리를 일정한 크기의 공간으로 나누어 관리하는 단위이다.
| 용어 | 설명 |
|---|---|
| page (p) | 논리 메모리를 일정한 크기로 나눈 블록 |
| frame (f) | 물리 메모리를 일정한 크기로 나눈 블록 |
| offset (d) | page나 frame을 동일한 크기로 자른 것 (두 공간에서의 offset 크기는 동일) |
➡️ frame크기 = page 크기
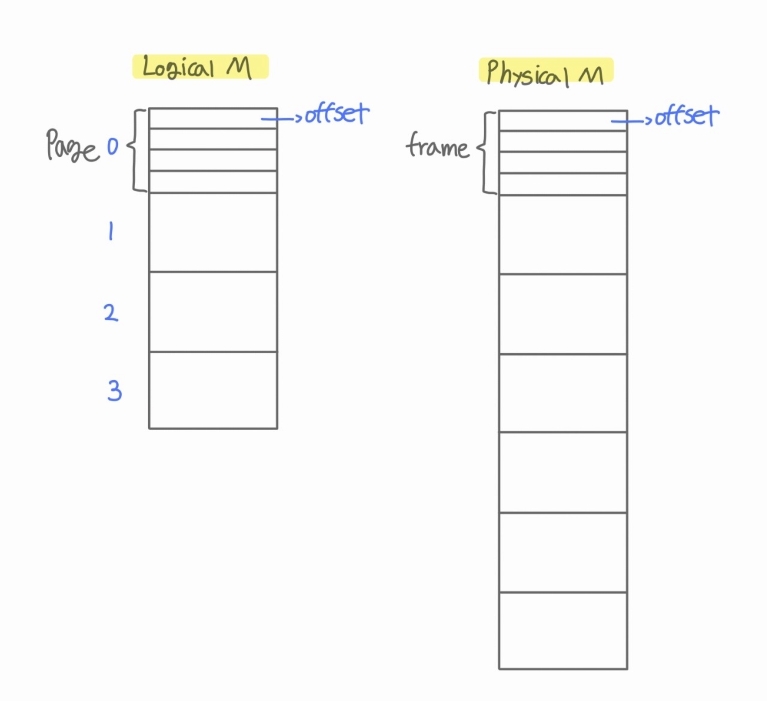
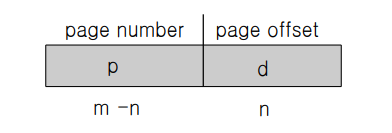
주소를 넘겨줄 때 페이지 번호 (p)와 오프셋 (d)만 넘겨주면 된다.
- “p 페이지에 있는 d번째 메모리에 할당해 줘”
- 프로세스마다 페이지의 개수가 다르기 때문에 페이지 테이블을 통해 관리해 주어야 한다.
3.2 페이지 테이블
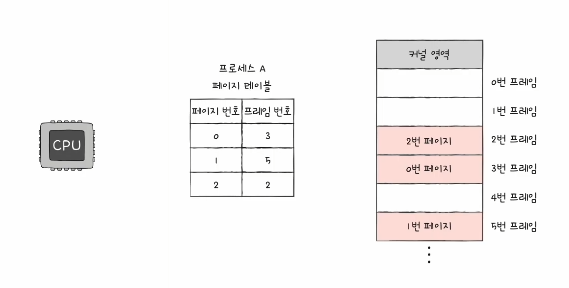
페이지 테이블을 통해 p와 f를 짝지어 주어 물리 주소(실제 메모리 주소)에 불연속적으로 배치되더라도 논리 주소(CPU가 바라보는 주소)에는 연속적으로 배치되도록 한다.
- CPU는 그저 논리 주소를 순차적으로 실행하면 된다.
- 즉, 페이지 테이블은 페이지 번호와 프레임 번호를 짝지어 주어 논리 주소 값이 물리 공간의 어느 위치에 놓아질지 결정해준다!
- 페이지 테이블은 프로세스마다 존재한다.
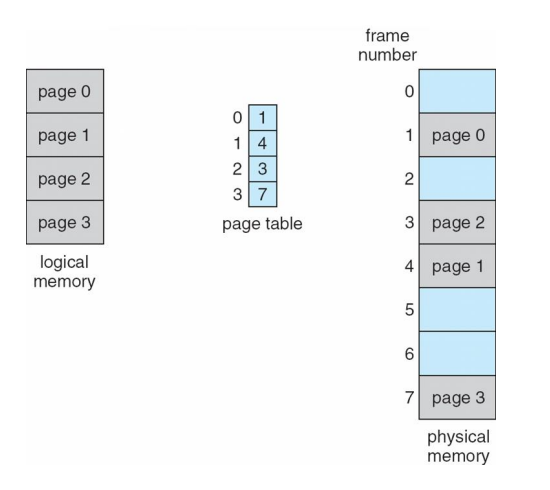
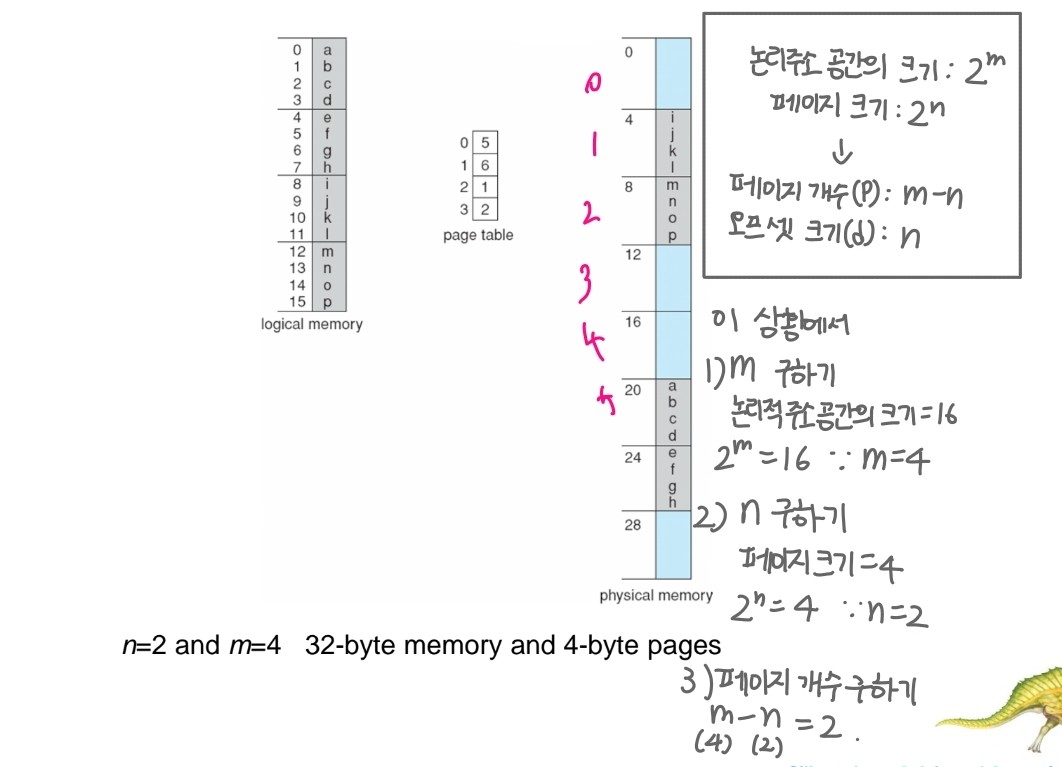
페이징 예시
- n, m 값을 구해보자.
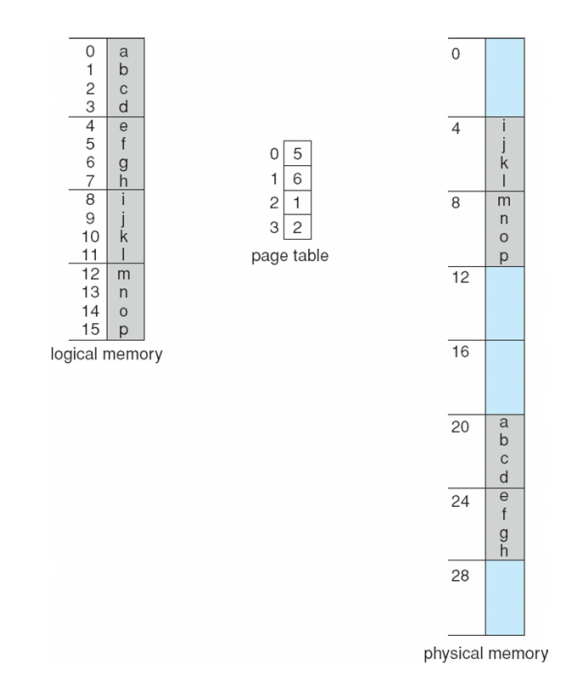
- 논리 주소 공간의 크기가 2ᵐ이고 페이지 크기가 2ⁿ인 경우 페이지의 개수는 m−n, 오프셋 크기는 n이다.

댓글남기기